サイコロをつくる

この記事はTCU-CTRL場外乱闘 Advent Calendar 2017 19日目の記事です。

備忘録でもあるので表現がくどいかもしれない。

やること

ロジスティック写像を使って6面サイコロを作ってみましょう。

下準備

\begin{align}
\label{eq:logistic} x_{t+1}=ax_{t}(1-x_{t})
\end{align} 
式\eqref{eq:logistic}のような漸化式をロジスティック写像と呼びます。 x_{t}は現時点の状態値を表します。写像に与える初期値 x_{0}は通常 0 \leq x_{0} \leq 1から選びます。また、 a=4のときに写像はカオス的な振る舞いをします。本記事では a=4とします。

さっそく式\eqref{eq:logistic}に代入してみましょう。以下、写像やロジスティック写像は式\eqref{eq:logistic4}を指します。
\begin{align}
\label{eq:logistic4} x_{t+1}=4x_{t}(1-x_{t})
\end{align}
式\eqref{eq:logistic4}は次のような特徴をもちます。

  • 決定論的：現在の状態 x_{t}から未来の状態 x_{t+1}が一意に定まる
  • 有界性：入力値 x_{t}が 0 \leq x_{t} \leq 1ならば出力値 x_{t+1}は 0 \leq x_{t+1} \leq 1となる
  • 非周期的：同じ値を繰り返さない
  • 初期値鋭敏依存性：異なる初期値に対してはまったく別の振舞いをする

つまりどういうことか

範囲[0,1]から適当に初期値をとってきてロジスティック写像を繰り返し適用すれば範囲[0,1]の値を重複なしでわりと無秩序に生成できる。乱数みたいだねすごいね。

サイコロをつくる

ロジスティック写像を使えば範囲[0,1]の値 x_{t}を得られる。区間[0,1]を6等分するような閾値を求め、各区間にサイコロの出目を割り当てればよさそうである。以下、 x_{t}に対応するサイコロの出目を y_{t}とする。

イメージとしては下の図のような感じです。

f:id:henceee:20171217000143p:plain:w400

f:id:henceee:20171214021624j:plain:w300

まだ理解できない大先輩のために具体例を示します。

  • x_{t}=0.1919・・・\displaystyle \frac{1}{6} \leq x_{t} \lt \frac{2}{6} なので y_{t}=2
  • x_{t}=0.810・・・\displaystyle \frac{4}{6} \leq x_{t} \lt \frac{5}{6} なので y_{t}=5
  • x_{t}=1.14514・・・ 0 \leq x_{0} \leq 1ならこんなことは起きない





f:id:henceee:20171214021633j:plain:w300

完璧ですね。

数値実験

 初期値 x_{0}=0.114514とし、ロジスティック写像を100万回適用する。 x_{t}を y_{t}に変換し、100万回中の出目1~6の出現回数を測定する。実験結果は以下の通りです。

出目 y_{t}
1
2
3
4
5
6
出現回数 269244 123692 108108 108273 123183 267500
割合(%) 26.9 12.3 10.8 10.8 12.3 26.7

はいうんこ
サイコロなのに出目に偏りがある。原因はなにか。なんでしょうね？

原因

原因はずばり確率密度関数にある。
ロジスティック写像によって得られる値の出現確率は式\eqref{eq:pkakuritu}の確率密度関数に従うことが知られている。
\begin{align}
\label{eq:pkakuritu} p(x)=\frac{1}{\pi \sqrt{x(1-x)}}
\end{align} 
式\eqref{eq:pkakuritu}の概形は以下の通りです。

f:id:henceee:20171210223458p:plain
式\eqref{eq:pkakuritu}の概形
形状からわかるように定義域の端ほど値が出現しやすく、中央に向かうにつれて出現しづらくなる。

つまりどういうことか

ロジスティック写像から得られる値の出現頻度に偏りがあるのでそのまま一様乱数として用いることはできない。

サイコロをつくる・その２

確率密度関数 p(x)を考慮し、改めて閾値を求める。
p(x)が確率密度関数であるならば定義域内の面積は1となる。一応確かめてみる。やっちまってくださいWolframAlpha兄貴。
www.wolframalpha.com
f:id:henceee:20171210231046g:plain
はいありがとうございます。問題なさそうです。

面積が1であることが確認できたので、この面積を6等分するような閾値を探す。具体的には以下の条件を満たすパラメータ a_{1}～a_{5}を探す。

\begin{align}
\label{eq:jk1} 0 \lt a_{1} \lt a_{2} \lt a_{3} \lt a_{4} \lt a_{5} \lt 1
\end{align} 


\begin{align}
\label{eq:jk2} \int_0^{a_{1}} p(x) dx = \int_{a_{1}}^{a_{2}} p(x) dx = \int_{a_{2}}^{a_{3}} p(x) dx = \int_{a_{3}}^{a_{4}} p(x) dx = \int_{a_{4}}^{a_{5}} p(x) dx = \int_{a_{5}}^{1} p(x) dx = \frac{1}{6}
\end{align}

くどいかもしれませんがイメージとしては下図のように確率密度関数の面積を6等分するパラメータです。色のついた部分の面積はそれぞれ \frac{1}{6}となります。
f:id:henceee:20171213165821p:plain

見つけました。詳細は補足を参照してください。

パラメータ a_{1} a_{2} a_{3} a_{4} a_{5}
値 0.066 0.25 0.5 0.75 0.933

x_{t}から y_{t}への変換は下図のようになる。
f:id:henceee:20171217000147p:plain:w400

なぜこんなことをするのか

いきなり確率密度関数とか言われてもしらねーよカスという人のためにガバガバ解説を載せときます。問題なさそうな人は飛ばしてください。

数値実験・その２

閾値 a_{1}～a_{5}を元に数値実験を行う。先ほどと同じく初期値 x_{0}=0.114514とし、ロジスティック写像を100万回適用した。実験結果は以下の通りです。

出目 y_{t}
1
2
3
4
5
6
出現回数 166340 168264 166440 166258 165635 167063
割合(%) 16.6 16.8 16.6 16.6 16.5 16.7

出目の出現回数がほぼ均等になっている。

無事ロジスティック写像によりサイコロの作成に成功し







f:id:henceee:20171211004020p:plain:w300

問題点


出現回数的には問題なさそうだが、実は出目の出現位置に問題がある。
意味不明なので具体例を示す。まずは下の表を見てもらいたい。

y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 27575 27872 27634 27662 27949 27987
2
 27669 27607 27649 27961 27694 27526
3
 27934 27568 27719 27816 27756 27694
4
 27701 27729 27761 27602 27901 28084
5
 28051 27550 27928 28021 27695 27867
6
 27749 27780 27797 27716 28117 27678

これは一様乱数を用いて作成したサイコロを100万回振った際のデータである。行は t回目の出目、列は t+1回目の出目を表す。サイコロを100万回振った結果{ y_{1},y_{2},...,y_{1000000}}について隣接する2要素 y_{t}と y_{t+1}の関係を調べた。例えば表内の赤文字をみると、2のあとに3が出た回数が27649回であったことがわかる。
値が均等に分散しているため、出目の間に相関性(「×が出た後は□がでやすい」といった傾向)がないことがわかる。

数値実験・その２では確率密度関数を6分割したことにより出目の出現回数が均等になったことを確認した。では出目の相関性はどうだったのか。調べた結果が以下の通りです。

y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 83338 83002 0 0 0 0
2
 0 1214 83642 83408 0 0
3
 0 0 0 0 83005 83435
4
 0 0 0 0 82630 83628
5
 0 0 82785 82850 0 0
6
 83002 84047 13 0 0 0


f:id:henceee:20171213184854p:plain
尋常ではない結果となった。このサイコロでは1が出た直後は3~6が出ず、1か2が出るようだ。他の出目についても強い相関関係があるらしい。
原因はなんでしょうね？

原因

原因は式\eqref{eq:logistic4}のロジスティック写像にある。
簡単に言うと、ロジスティック写像では x_{t}が0付近の場合に x_{t+1}も0付近の値に、 x_{t}が1付近の場合に x_{t+1}は0付近の値になるといった特徴があり、前後する状態値は強い相関関係をもつ。 y_{t}は x_{t}を閾値 a_{1}～a_{5}によって単純に変換した値であるため、 x_{t}と x_{t+1}の相関が y_{t}と y_{t+1}にも影響する。この相関をどうにかしないとまともなサイコロとして機能しないわけである。

解決策

力技的な解決方法として出目の結果{ y_{1},y_{2},...y_{t}}をシャッフルするというものがある。乱数を生成するために乱数を用いるのである。これもうわかんねぇな

もう少しよさげな方法として x_{t+1}を離れたところから持ってくるというものがある。ロジスティック写像では写像を適用した回数が増えると相関が弱まることが知られている。具体的には x_{t}と x_{t+1}には強い相関があるが、 x_{t}と x_{t+100}の間に相関はほぼない。ならば x_{t+100}を x_{t+1}として採用してしまえばよい。

ここで、関数 f^{n}(x_{t})を定義する。 f^{n}(x_{t})は引数の x_{t}にロジスティック写像を n回適用し結果 x_{t+n}を返す関数である。実装は再帰なりループなりでどうぞ。
こいつはこんな風に使う。

\begin{align}
\label{eq:logisticn} x_{t+1}=f^{n}(x_{t})
\end{align}

nの値を調節することで2要素 x_{t}と x_{t+1}の相関性を操作できるわけである。 nが小さいなら相関性は強く、大きいなら相関性は弱くなる。

数値実験・その３

相関性を考慮した実験を行った。初期値 x_{0}=0.114514とし閾値は数値実験・その２と同じく a_{1}～a_{5}を用いた。状態値の更新は式\eqref{eq:logisticn}の f^{n}(x_{t}により100万回行い、 n=2,5,10について調べた。
実験結果は以下の通りです。出目の出現回数は省きました。

  • n=2
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 41618 42225 41989 40417 0 0
2
 0 0 0 1176 83275 83555
3
 41496 41862 41181 41697 0 0
4
 41321 42091 41460 41130 0 0
5
 0 0 0 0 83373 83289
6
 41814 41827 41606 41582 15 0
  • n=5
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 26009 26617 26029 26190 29728 31084
2
 30854 31368 31470 31343 22149 20888
3
 25998 26248 25845 25618 31217 31190
4
 26074 26228 25844 26388 31330 31076
5
 30788 31500 31210 31340 20716 20937
6
 25934 26110 25719 26061 31351 31548
  • n=10
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 27722 27902 27344 27678 27749 27616
2
 27641 28204 27972 27975 27934 28031
3
 27544 28115 27732 27764 27620 27458
4
 27733 27944 27868 27856 27707 27559
5
 27530 27838 27720 27708 27967 28066
6
 27841 27754 27597 27686 27852 27772




f:id:henceee:20171214001227j:plain
実験結果にご満悦の先輩


nの値を増やすと x_{t}と x_{t+1}の相関性が弱まり、出目 y_{t}と y_{t+1}の相関も弱まるようだ。

結論

写像の適用回数を調節し、隣接する2つの要素 x_{t}と x_{t+1}の相関性を弱めることができた。隣接する要素数が3つや4つの場合は未調査ですが、 n=50くらいにするといい感じの一様乱数になるそうです。
以上でロジスティック写像を用いてサイコロを作れたことにします。ここまでありがとうございました。

次回はジコリーニョ君です。よろしくお願いします。

補足


確率密度関数の面積を6等分するパラメータ a_{1}～a_{5}については数値積分により求めた。式\eqref{eq:pkakuritu}の p(x)の面積は1であるから、計算中の面積が \frac{1}{6}を超えた瞬間の xを a_{1}に、 \frac{2}{6}を超えた瞬間の xを a_{2}に割り当てるといった感じである。

蛇足

だが待ってほしい。本当にこれでいいのだろうか？

問題点

冒頭でロジスティック写像の特徴として非周期性(同じ値を繰り返さない)を紹介した。しかし現実では小数を有限桁で扱うため、写像が出力可能な値のパターンにも限りがあり周期が生まれてしまう。
話は変わるがさきほどは x_{t}と x_{t+1}の相関をなくすために関数 f^{n}(x_{t})を用いた。初期値 x_{0}の更新に f^{10}(x_{t})を使うと、 x_{1}には x_{10}が、 x_{2}には x_{20}が割り当てられる。要するにこの方法では写像が出力可能なパターン数を n倍で消費してしまうわけである。
なんかもったいないと思いませんか？思いますよね。なのでここから先は nを小さくしつつ隣接する2要素 y_{t}と y_{t+1}の相関性を弱める方法について検討します。

分割数の変更

下の画像を見てほしい。
f:id:henceee:20171213165821p:plainf:id:henceee:20171217000147p:plain:w400
現在のサイコロは式\eqref{eq:pkakuritu}の確率密度関数 p(x)を6分割する5つのパラメータ a_{1}～a_{5}について昇順にサイコロの出目{1～6}を割り当てている。だが p(x)の面積を6分割できているなら出目の割り当て順がどんなんであっても出目の出現回数は変わらないはずである。また領域が連続である必要もない。

意味不明なので具体例を示す。
p(x)を12分割する11個のパラメータ a_{1}～a_{11}を下のような条件で定める。

\begin{align}
\label{eq:jk3} 0 \lt a_{1} \lt a_{2} \lt ... \lt a_{10} \lt a_{11} \lt 1
\end{align} 


\begin{align}
\label{eq:jk4} \int_0^{a_{1}} p(x) dx = \int_{a_{1}}^{a_{2}} p(x) dx = ... = \int_{a_{10}}^{a_{11}} p(x) dx = \int_{a_{11}}^{1} p(x) dx = \frac{1}{12}
\end{align}
この11個のパラメータについて下のようにサイコロの出目を割り当てる。
f:id:henceee:20171217000139p:plain

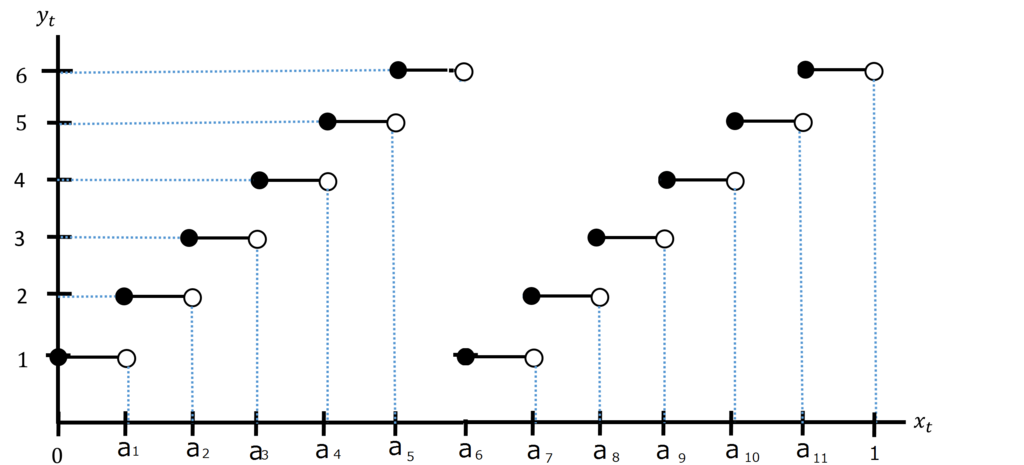
出目が1となるような x_{t}の区間は [0,a_{1})と [a_{6},a_{7})である。では p(x)上でこの区間の和はどうなるのか。
\eqref{eq:jk4}から

\displaystyle \int_0^{a_{1}} p(x) dx + \int_{a_{6}}^{a_{7}} p(x) dx = \frac{1}{12} + \frac{1}{12} = \frac{1}{6}

他の出目についても区間の和は \frac{1}{6}となる。図のように1つの出目についての区間が不連続でも p(x)についての面積が等しいので各出目の出現回数は等しくなるはずだ。ここまでは先ほどの6分割と変わらない。何が変わったのか？

6分割の場合、出目が1となるのは x_{t}が0付近のときであり、出目が6となるのは x_{t}が1付近のときであった。しかし、12分割の場合は x_{t}が定義域 [0,1]の中心付近のときでも出目が1や6になる場合がある。つまり分割数を増やすほど、以前と比較して様々な区間に出目をばらまくことが可能となるわけである。

x_{t}と x_{t+1}を従来の6分割で y_{t}と y_{t+1}に変換すると相関が残ってしまう。分割数を増やし、区間に対する出目の割り当て方を変更することで、 y_{t}と y_{t+1}にある相関を弱めたいわけである。

出目の割り当て

ここでは2つの割り当て方法を紹介する。

1つ目は先ほどの12分割の画像のようにパラメータに対し昇順にサイコロの出目{1～6}を割り当てる方法である。この割り当て方法を通常割り当てと呼ぶことにする。

2つ目は乱数による割り当てであり、各パラメータに対してランダムにサイコロの出目{1～6}を割り当てる方法である。ランダムとはいえ各出目を割り当てる回数を揃えることで p(x)での面積が均一になり、出目の出現回数は等しくなる。この方法をランダム割り当てと呼ぶことにする。

結局乱数使ってるじゃねーかハゲという指摘もあると思うが乱数を用いるのはパラメータに対する出目の割り当てのみである。状態値の更新や y_{t}への変換では使用しないので多分レギュレーション違反ではないと思います。

数値実験・その４

分割数と割り当て方法の効果を確認する実験を行った。初期値 x_{0}=0.114514とし、状態値の更新はロジスティック写像により100万回行った。ロジスティック写像により更新を行うため、 x_{t}と x_{t+1}の間には相関が残る。分割数は 6^{1},6^{2},6^{5}とし、それぞれ通常割り当てとランダム割り当てについて調査した。

  • 分割数 6^{1}、通常割り当て
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 83338 83002 0 0 0 0
2
 0 1214 83642 83408 0 0
3
 0 0 0 0 83005 83435
4
 0 0 0 0 82630 83628
5
 0 0 82785 82850 0 0
6
 83002 84047 13 0 0 0

当然だが以前と同じ結果である。ランダム割り当ては割愛します。

  • 分割数 6^{2}、通常割り当て
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 41961 41835 0 0 41980 41513
2
 0 0 83171 83329 0 0
3
 41715 41575 0 0 41701 41717
4
 42273 41525 0 0 41602 41277
5
 0 0 83537 83348 0 0
6
 41340 41564 0 0 41603 41433

分割数を増やしただけで多少はマシになった。

  • 分割数 6^{2}、ランダム割り当て
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 0 27849 27635 41903 41938 27985
2
 69895 14052 27671 27887 0 27448
3
 27803 41970 14110 13809 41321 27388
4
 28112 55328 55579 0 13765 13809
5
 41500 13798 14018 27708 27774 41785
6
 0 13956 27388 55287 41785 27743

だいぶマシになったがまだ0が存在する。

  • 分割数 6^{5}、通常割り当て
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 41307 41613 0 0 41687 41350
2
 0 0 83132 83378 0 0
3
 41540 41304 0 0 41770 41770
4
 41794 41979 0 0 41873 41597
5
 0 0 83252 83865 0 0
6
 41317 41614 0 0 41786 42071

分割数を増やすだけではあまり改善しない。

  • 分割数 6^{5}、ランダム割り当て
y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 29063 26831 28954 26837 28333 26328
2
 24961 30363 28250 29894 26429 26461
3
 29508 26861 26127 26012 29579 28203
4
 28146 28696 28974 26768 26423 27448
5
 25746 26592 26996 28067 28631 31016
6
 28922 27015 26989 28877 27653 28046

分割数を増やし、ランダム割り当てを行うことで大幅に改善した。

まとめ

数値実験・その４では状態値の更新にロジスティック写像を使っている。これは状態値の更新に n=1とした関数 f^{n}(x_{t})を用いたのと同じ意味である。実験により、 n=1であっても確率密度関数の分割数を増やし、分割した区間に対してランダムにサイコロの出目を割り当てれば y_{t}と y_{t+1}の相関を弱められることを確認した。

改善を確認したのはあくまで隣接する2つの要素 y_{t}と y_{t+1}についてである。3つや4つの要素間には相関が残っているかもしれないしこの手法を用いても nの値は増やすべきだと思う。ただ nを増やす度合いはこちらのほうが少なくて済む気がする。

補足・その２

最良結果

実は 6^{7}分割の結果もある。載せる場所がないのでここに置いときます。
初期値 x_{0}=0.114514、状態値はロジスティック写像により100万回更新、出目はランダムに割り当てた。

y_{t} \ y_{t+1}
1
2
3
4
5
6
1
 27670 27848 27678 27730 27328 27750
2
 27884 27466 27859 27950 27311 27859
3
 27544 27883 28319 27928 27875 27673
4
 27707 27878 27732 27459 27911 27802
5
 27556 27537 28060 28022 27714 27764
6
 27644 27717 27574 27400 28514 28453

結果だけみると一様乱数を用いたやつとあまり変わらないように見える。

計算量

ところで 6^{7}=279936である。確率密度関数を 6^{7}分割するパラメータは a_{1}～a_{279935}の279935個であり、状態値 x_{t}が更新されるたびに x_{t}がどの区間に当てはまるかを計算する必要がある。
愚直にプログラムを組むと計算量は O(更新回数×分割数)となりなんだか時間がかかりそうである。だがパラメータは条件式\eqref{eq:jk1}のようにインデックスに従って昇順になっているから二分探索を用いることができる。
要するに何が言いたいかというと分割数が増えてもさほど問題はない。ただパラメータを配列で管理する必要があるためメモリがやばいかもれしない。

パラメータの求め方

さっきはパラメータを数値積分により求めたと説明したな。



f:id:henceee:20171218023453j:plain:w300

6^{7}分割の場合は約28万個のパラメータが必要となる。これを数値積分により求めるのはしんどそうである。もう少し楽な方法を検討する。

確率密度関数 p(x)はこのような式であった。

\displaystyle p(x)=\frac{1}{\pi \sqrt{x(1-x)}}

とりあえず p(x)を積分する。( logの底はeです)　
いつもありがとうございます、兄貴


f:id:henceee:20171217170639g:plain


積分定数を0とし右辺を P(x)とおく。つまり
\begin{align}
\label{eq:Px} P(x)=\frac{2 \sqrt{x-1} \sqrt{x} \log(\sqrt{x-1}+\sqrt{x})}{\pi \sqrt{-(x-1)x}}
\end{align} 
となる。
ここで P(x)の形状は下図のようになる。

f:id:henceee:20171217171620g:plain

図から P(0)=-1,P(1)=0であり、[0,1]では xが増加すると P(x)も増加する。
\displaystyle P(x)=- \frac{5}{6}を満たす xを bとすると、 xが0からbに変化する間に P(x)は\displaystyle -1から-\frac{5}{6}に、すなわち\displaystyle \frac{1}{6}だけ増加した。

x:0→bで P(x)の変化量の和が\displaystyle \frac{1}{6}であるため

\begin{align}
\label{eq:Pint} \int_0^{b} P'(x) dx = \frac{1}{6}
\end{align} 

となる。ここで、 p(x)を積分したものが P(x)であるから P(x)の微分は p(x)になる。

\begin{align}
\label{eq:Pin} \int_0^{b} p(x) dx = \frac{1}{6}
\end{align} 

つまり確率密度関数 p(x)の[0,b]の面積が\displaystyle \frac{1}{6}であることがわかる。

くどいようだがもう少し説明する。\displaystyle P(x)=- \frac{4}{6}となるような xを cとすると、 x:b→cで P(x)の変化量の和が\displaystyle \frac{1}{6}であるため

\begin{align}
\label{eq:pp} \int_b^{c} P'(x) dx = \frac{1}{6}
\end{align} 

となり、

\begin{align}
\label{eq:ppp} \int_b^{c} p(x) dx = \frac{1}{6}
\end{align} 

となる。つまり確率密度関数 p(x)の[b,c]の面積が\displaystyle \frac{1}{6}であることがわかる。

要するに\displaystyle P(x)=-\frac{5}{6},...,-\frac{1}{6}を満たす5つの xを見つければ、確率密度関数を6等分する閾値が求まるのである。\displaystyle P(x)=-\frac{35}{36},...,-\frac{1}{36}について解けば36等分、\displaystyle P(x)=-\frac{215}{216},...,-\frac{1}{216}について解けば216等分の閾値が求まる。

上記の方法は研究室の強い人たちに教えてもらった。改めて感謝する。

P(x)についての方程式を解けば閾値(パラメータ)を求めることができるが、パラメータ数が増えると兄貴にいちいちコピー＆ペーストするのが辛くなる。欲を言えば結果はファイルに出力してプログラムで使いたい。というわけで計算には学校で利用できるMathematicaを使用した。Mathematicaならプログラミングが可能であるため、 P(x)についての方程式をループで解いて結果をファイルに出力できる。

だがしかしうまくいかない。これは自分のMathematicaに関する知識不足が原因なのだが、分割数が増えると右辺の定数によっては方程式を解いてくれない場合がある。Mathematicaと乱闘対話すること数時間、結果として以下の式を得た。
\begin{align}
\label{eq:yyy} a_{k}=\frac{1}{4} (2+(-1)^{\frac{n-k}{n}}-(-1)^{\frac{k}{n}})
\end{align} 
式\eqref{eq:yyy}は確率密度関数 p(x)を n等分する n-1個のパラメータ a_{k},(k=1,2,3,...,n-1)の一般項である。また、 0 \lt a_{k} \lt a_{k+1} \lt 1 ,(k=1,2,3...,n-2)となる。
多分 nが奇数でも偶数でも使えると思います。
本記事で用いた p(x)を分割するパラメータは全て\eqref{eq:yyy}により求めた。

以上で終わります。ここまでありがとうございました。